14 Bias-variance trade-off
This is a big topic in machine learning in general but only has had a handful of questions on PA. Without stating this explicitly as “the bias-variance tradeoff,” you have already been using this concept. We first need some definitions:
Mean Squared Error (MSE):
The sum of the squared difference between the predictions and target.
Variance of model:
The variance of the parameters, \(var(f(X))\). When variance is high, the model is often overfitting.
Bias:
The difference between the expected value of the estimate and the actual expected value. When the bias is high, the model is under fitting and is not complex enough to capture the signal in the data.
\[\text{Model Bias} = E(Y) - f(X)\]
Irreducible Error:
Random noise in the data that can never be understood. This is “irreducible,” meaning that the model cannot reduce it, but you can reduce it by cleaning the data, transforming variables, and engineering additional features.
The Bias-variance trade-off says that when the bias of the parameter estimates increases, the variance decreases, and vice versa as the bias decreases.
\[\text{MSE} = \text{Variance of model} + \text{Bias}^2 + \text{Irreducible Error}\] Your goal is to make the MSE as small as possible. When you test different models, tune parameters, and perform shrinkage or variable selection, you change the bias and the variance.
A helpful way to remember this relationship is with the following picture. Imagine that you are at a shooting range and am firing a pistol at a target. Your goal is to get as close to the center of the bullseye as possible.
Ideally, your bullets would have low bias and low variance (upper left). This would mean that you consistently hit the center of the target. In the worst case, your bullets would have high bias and high variance (lower right). You would be changing your aim between shots and would not be centered at the bullseye.
The other diagonals (lower left and upper right) are the more common outcomes. Either you keep your arm steady and do not change your aim between shots but miss the center, or you move around too much and have high variance.
You can decrease the variance by using more data. From Exam P, you may remember that the variance of the sample means decreases as the square root of \(N\), the sample size, increases. To decrease the bias, you can change the type of model being used.
Model flexibility is the amount that the model can change. The easiest way to understand flexibility is in the case of the linear model. A GLM with 1 predictor has low flexibility.
A GLM with 100 predictors has high flexibility. This is a general definition because you technically need to consider the size of the coefficients as well. It is easy to confuse flexibility with the variance of model, but the two concepts are different. In this GLM example, the variance would be determined by the standard errors on the coefficients.
A model with high variance would have large p-values, but this could still be inflexible if only a few predictors are included. Conversely, a model could have high flexibility by having many predictor variables and interaction terms but have low variance if all of the p-values were small.
Your goal of PA is to solve a business problem. There is a constant balance between making an interpretable model and one that has good performance. Highly flexible models, which are often called black boxes, are only useful for making predictions.
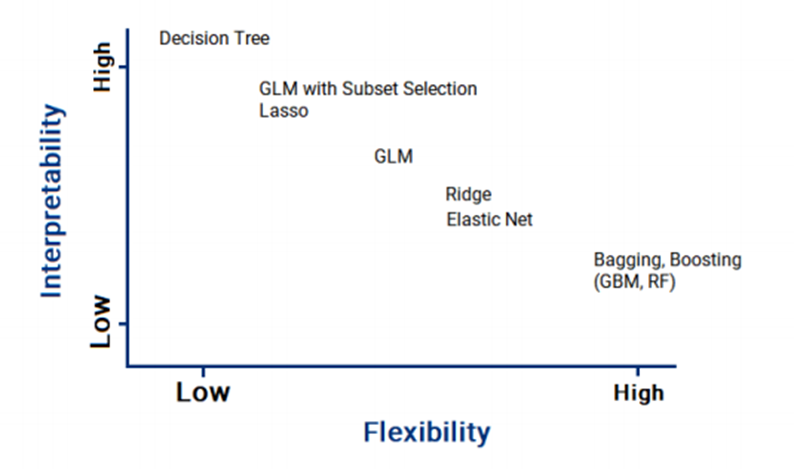
The parameters that you change also have an impact. In the case of the lasso or ridge regression, by increasing \(\lambda\) you can decrease the flexibility. For stepwise selection, the value of k controls the amount by which the log-likelihood is adjusted based on the number of parameters. As you will see in the next chapter on trees, decision trees have flexibility adjusted by CP, and random forests (RFs) and gradient boosted machines (GBMs) have their parameters.